Summary
This application note shows the use of EnFuzion for modeling laser-atom collisions. EnFuzion contributed to this research by

 

• enabling the distribution of this application across idle machines without consideration of parallel or distributed programming practices
• shortening the time needed to solve QED equations
• facilitating the generation of detailed presentations of all possible data produced by the computations

 

What is modeling of laser-atom collisions?
A detailed understanding of the collision processes between atoms, electrons and ions is of great interest to the atomic physics community. This knowledge is important in the explanation of laboratory and astrophysical plasmas, spectroscopic and surface collision physics, and scattering dynamics. Applications include fluorescent lamp and gas laser technology, surface science, and atmospheric physics.

 

Of particular interest is the investigation of electron collisions with a short-lived, laser-excited target atom. Currently, there are two experimental methods for exploration of the electron-excited atom collision process:

 

• electron-photon coincidence method
• electron-superelastic scattering technique

 

The electron-photon coincidence method detects a fluorescence photon from the electron excited state after polarization analysis in coincidence with the inelastically scattered electron that was responsible for excitation.

 

In the electron-superelastic scattering technique, an atom is optically prepared by a laser of known polarization in an excited state; scattered electrons, which gain energy by collisionally de-exciting the atom, are detected.

 

Electron-superelastic technique requires a detailed understanding of the laser-atom interaction as a function of laser intensity, laser polarization and laser/atom detunings. It is possible, using Quantum Electrodynamic (QED) theory, to generate equations of motion for atomic operator elements representing atomic populations in the ground and excited state, optical coherences formed between the ground and excited state by the laser, and excited state coherences formed by the laser. The QED model generates closed sets of coupled, first order, linear, homogeneous differential equations. These equations are solved using numeric integration, which can be time consuming.

 

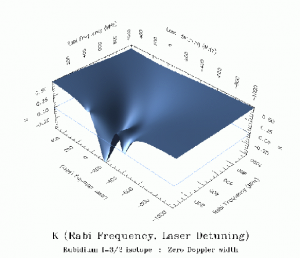
Once the dynamics of the atomic operators are known, it is theoretically possible to predict the line polarization (K) for linearly polarized excitation, or the optical pumping parameter (K’) for circularly Polaris excitation. It is how these parameters vary as a function of laser intensity and detuning that is of particular interest to physicists. Introducing integration over the Doppler profile of the atomic beam introduces another complexity which further lengthens the computing time needed.

 

How did using EnFuzion help with modeling laser-atom collisions?
EnFuzion enabled distribution of this application across idle machines without consideration of parallel or distributed programming practices. EnFuzion shortened the time needed to solve QED equations. It also helped generate detailed presentations of all possible data produced by the computations.

 

How was EnFuzion used?
The following plan file was used to control the experiment:

 

parameter doppler text select oneof "Non-Doppler" "Doppler"
    default "Non-Doppler";
parameter isotope text select oneof "Isotope1" "Isotope2" default "Isotope2";
parameter circular text select oneof "Linear" "Circular" default "Linear";
parameter dmin label "Detuning Minimum" integer default 1;
parameter dmax label "Detuning Maximum" integer default 1;
parameter dnpt label "Detuning Number of Points" integer default 1;
parameter laseri label "Laser Intensity" integer range from 1 to 1 step 1;
parameter dwidth label "Laser Width" integer range from 1 to 1 step 1;

task nodestart
    copy input.generic node:.
    copy qed.sh node:.
endtask

task main
    node:substitute input.generic input
    node:execute qed.sh $laseri $Doppler $isotope $circular \
        $dmin $dman $dnpt $dwidth
    copy node:data.$laseri .
endtask

 

The following figure shows K and K’ plotted as a function of laser intensity and laser detuning at the same time. A third variable, the Doppler width of the atomic beam, can be introduced and, with the current software three-dimensional plots, can now display K and K’ as functions of laser intensity, detuning and atomic beam Doppler width. This allows the most detailed presentation of all possible data produced by these computations which covers all experimental conditions currently under investigation.

 

See [Abramson D., Sosic R., Giddy J. and Hall B., Nimrod: A Tool for Performing Parametised Simulations using Distributed Workstations, The 4th IEEE Symposium on High Performance Distributed Computing, Virginia, August 1995.] for more details.

 

 

Further Information
This application note describes some capabilities of EnFuzion.  For more information on EnFuzion, please refer to the EnFuzion User Manual.